SUPRACONDUCTIVITÉ

SUPRACONDUCTIVITÉ

La résistance électrique de certains conducteurs devient brutalement inférieure à toute valeur mesurable au-dessous d’une certaine température T ^c dite température critique . On dit qu’il y a transition du conducteur de l’état normal (noté N) à l’état supraconducteur (noté S). Dans un conducteur à l’état S, un courant électrique peut donc circuler sans aucune dissipation d’énergie. De plus, un champ magnétique extérieur suffisamment faible ne peut pas pénétrer dans la masse d’un échantillon macroscopique. Ces deux propriétés complémentaires sont dues à l’établissement, au-dessous de T ^c d’un «état ordonné» des électrons de conduction dû à l’existence d’une interaction attractive entre les électrons.

À température inférieure à T ^c, dans les supraconducteurs dits de première espèce, ces deux propriétés sont observées jusqu’à une valeur critique H ^c du champ magnétique au-delà de laquelle l’état supraconducteur disparaît; dans les supraconducteurs dits de deuxième espèce, plus intéressants du point de vue technologique, il existe un domaine de champs magnétiques élevés, pour lesquels l’échantillon est dit à l’«état mixte», où l’on observe une pénétration partielle du champ et où le passage d’un courant peut s’accompagner d’effets dissipatifs.

Des développements théoriques et expérimentaux considérables ont été obtenus depuis 1957, et ont été reconnus par l’attribution du prix Nobel de physique, en 1972, à John Bardeen, Leon N. Cooper et John R. Schrieffer (B.C.S.) pour la théorie microscopique de la supraconductivité; en 1973, à Ivar Giaever pour la mise en évidence directe de cette théorie et à Brian D. Josephson, qui avait dégagé le rôle de la phase dans l’ordre supraconducteur (sa prédiction a été à l’origine de toute une série d’applications en métrologie ultrafine). Cependant, la supraconductivité restait un phénomène observé aux très basses températures (inférieures à 23 K). En découvrant, en 1986, un oxyde à base de cuivre, lanthane et baryum devenant supraconducteur à 35 K, J. Georg Bednorz et K. Alex Müller (prix Nobel 1987) ouvrirent de formidables perspectives technologiques et scientifiques. De nouveaux matériaux (tels que l’oxyde HgBa²Ca²Cu³⁸) avec des T ^c aussi élevées que 135 K sont aujourd’hui synthétisés. La supraconductivité s’affranchit des techniques sophistiquées de basses températures réservées aux laboratoires, et des applications à grande échelle peuvent être envisagées. De nombreuses expériences sont réalisées pour comprendre les mécanismes fondamentaux de cette surprenante supraconductivité à haute température critique qui bouleverse le cadre théorique proposé par B.C.S.

1. Découverte et développement

La supraconductivité a été découverte en 1911 à Leyde (Pays-Bas) par Heike Kammerlingh Onnes, qui venait de réussir la liquéfaction de l’hélium (4,2 K). Mesurant la résistivité d’un barreau de mercure, il constata qu’au-dessous de 4,15 K celle-ci tombait brutalement à une valeur infiniment faible. Cette «superfluidité» des électrons est comparable à l’écoulement non visqueux de l’hélium ⁴He au-dessous de 2,17 K.

En 1933, Walther Meissner et R. Ochsenfeld ont étudié le comportement d’un barreau de métal pur (supraconducteur de première espèce) en présence d’un champ magnétique longitudinal h faible. Ils ont montré que, quelle que soit la façon d’opérer pour obtenir l’état supraconducteur en présence de h (trajets adb ou acb de la figure 1), l’induction B = 猪 ⁰(H + M ) est alors nulle à l’intérieur de l’échantillon. Ce diamagnétisme parfait, l’effet Meissner, ainsi que la superfluidité existent tant que le champ est inférieur à un certain champ critique fonction de la température (cf. physique des SOLIDES, Thermodynamique et chaleur spécifiques des solides ):

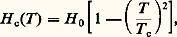où T ^c est la température critique, c’est-à-dire la température de transition en champ nul, et H ⁰ le champ critique à température nulle (cf. tableau).

L’effet Meissner ne peut pas s’expliquer par la seule hypothèse d’une conductivité parfaite, c’est-à-dire infinie. Pour un conducteur devenant parfait au-dessous de T ^c, on obtiendrait bien l’état final observé (B = 0 à l’intérieur de l’échantillon) en suivant le trajet adb mais non pas en suivant le trajet acb.

Fritz et Heinz London (1935) expliquent ces deux propriétés complémentaires, la superfluidité et le diamagnétisme parfait, par une théorie électromagnétique locale de la supraconductivité. Fritz London introduit le concept d’ordre à grande distance dans l’espace des impulsions ^{[cf. STATISTIQUE]} des électrons de conduction, à l’état supraconducteur, et prédit la quantification du flux magnétique qui sera observée en 1961. Par opposition avec le cas des métaux supraconducteurs purs, les mesures magnétiques sur des alliages montraient la possibilité de coexistence de l’état S et de champs magnétiques très élevés. Le concept d’éponge de flux magnétique (Kurt Mendelssohn, 1935) expliquait les irréversibilités rencontrées dans ces matériaux souvent inhomogènes, mais laissait de côté leurs propriétés réversibles. Celles-ci seront correctement observées en 1936 par Aleksei V. Shubnikov et expliquées par Aleksei A. Abrikosov en 1957: dans ces supraconducteurs, dits de deuxième espèce, l’effet Meissner existe jusqu’à un champ critique noté H ^c1, ou champ de première pénétration (courbe b dans la figure 2). Pour H 礪 H ^c1, un champ pénètre sous forme de «lignes de vortex» qui seront décrites plus loin (cf. chap. 4, Matériaux supraconducteurs ). La supraconductivité disparaît pour un champ critique supérieur H ^c2. Le calcul d’Abrikosov utilisait un modèle phénoménologique dû à Vitalü L. Ginzburg et Lev Davidovitch Landau (G.L., 1950), s’appuyant sur la description de Landau des transitions de phase du deuxième ordre (cf. changements de PHASE). L’état supraconducteur y est caractérisé par un paramètre d’ordre, comparable à la densité d’électrons supraconducteurs du modèle à deux fluides de Cornelis J. Gorter et Hendrik B. G. Casimir (1934), dont la signification était comprise par Abrikosov et L. P. Gorkov (A.G., 1960), à partir du modèle microscopique (B.C.S., 1957) fondé sur une remarque de Cooper: si l’on suppose une interaction attractive, aussi faible soit-elle, entre les électrons de conduction d’un métal, ceux-ci peuvent «s’ordonner» en un état plus stable – c’est-à-dire de plus faible énergie – que l’état normal en l’absence d’une telle interaction. Il expliquait ainsi la plupart des propriétés d’équilibre des supraconducteurs de première espèce (ceux qui sont décrits par la courbe d’aimantation a de la figure 2). Les descriptions de B.C.S., de G.L. et de A.G. constituent l’essentiel de la base théorique de ce sujet. L’état électronique d’un supraconducteur est constitué de paires d’électrons de moment d’impulsion et de spin opposés (paires de Cooper). La théorie de B.C.S. précisait la notion, introduite par Alfred B. Pippard (1953), de longueur de cohérence:

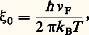où v ^F est la vitesse de Fermi du métal, k ^B la constante de Boltzmann, 寮 la constante de Planck divisée par 2 神; cette longueur mesure la taille d’une paire de Cooper, et elle est associée à la notion d’ordre à grande distance. Le modèle non local de Pippard conduisait à moyenner les effets de réponse électrodynamique dans un supraconducteur sur une distance 﨡 (fonction de 﨡⁰ et diminuant avec le libre parcours moyen électronique à l’état normal) par opposition au modèle local de London.

2. Modèle microscopique de B.C.S.

L’état d’ordre supraconducteur est analogue à celui d’un solide ou d’un composé ferromagnétique. La «rigidité» du supraconducteur devant des perturbations électriques ou magnétiques conduit à la conductivité infinie et à l’effet Meissner. L’interaction attractive entre les électrons d’une paire peut être décrite schématiquement. Un électron de conduction se déplaçant dans le métal provoque sur son passage une déformation locale du réseau cristallin par l’attraction qu’il exerce sur les ions positifs. Un deuxième électron sera soumis à l’excédent de charge positive qui a fait écran à la charge négative du premier électron. Celui-ci se déplace beaucoup plus vite que les ions (plus lourds): le deuxième électron sentira l’effet de la charge positive même quand le premier électron sera loin de lui. L’interaction entre les deux électrons a donc une grande portée. La température critique des supraconducteurs mous, dits à couplage fort, tels que le plomb, qui sont aussi de mauvais conducteurs à l’état normal, est élevée. Seule la fraction d’électrons dans une couche d’énergie de largeur 寮 諸^D (énergie de Debye, caractéristique des vibrations du réseau) autour de l’énergie de Fermi va être couplée en paires.

La température critique d’un supraconducteur varie comme l’indique l’expression:

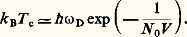Elle augmente de façon très rapide avec ⁰, densité d’état des électrons au niveau de Fermi, et avec le potentiel attractif V entre électrons. La prédiction la plus spectaculaire de B.C.S. est l’existence dans le spectre d’excitations d’une bande d’énergie interdite de largeur 2 = 3,52 k ^BT ^c, prévue à partir des mesures de chaleur spécifique à basse température qui s’annule comme

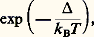aux très basses températures.

Giaever (1960) appliqua ses résultats sur l’effet tunnel entre deux métaux au cas des supraconducteurs et montra que l’on ne pouvait injecter des électrons dans un supraconducteur à très basse température qu’à partir d’un seuil en énergie correspondant à la bande d’énergie interdite.

En vue des utilisations industrielles, un effort important a été entrepris pour obtenir des températures critiques T ^c élevées selon les directions suivantes:

– augmenter la densité d’états électronique au niveau de Fermi; c’est le cas des alliages composés avec une structure A-15 (T ^c = 17,1 K pour V³Si, 23 K pour Nb³Ge, etc.),

– accroître le couplage entre les électrons et les phonons en modifiant les modes de vibrations du réseau cristallin.

La démarche la plus originale est certainement celle de W. A. Little (1964) proposant un nouveau mécanisme de couplage entre les électrons en utilisant des chaînes de molécules fortement polarisables qui conduisit à la découverte, en 1979, de la supraconductivité dans un conducteur organique synthétique [(TMTSF)²P⁶, di-tétraméthyl-tétrasélénofulvaline-hexafluorophosphate]. La température critique des composés organiques culmine actuellement à 12 K, à l’exception notable des dérivés des fullerènes C⁶⁰ (T ^c = 33 K pour Cs²RbC⁶⁰) [cf. POLYMÈRES CONDUCTEURS].

Même si les mécanismes responsables de la supraconductivité de ces matériaux et des composés à haute T ^c sont aujourd’hui controversés, les résultats expérimentaux montrent clairement l’existence d’un état ordonné des électrons fondé sur les paires de Cooper.

3. Paramètre d’ordre et expériences fondamentales

Le paramètre d’ordre, notion introduite à propos du modèle de G.L., est une fonction d’onde complexe qui décrit l’état quantique macroscopique dans lequel se trouvent condensées les paires de Cooper; son amplitude donne la probabilité de présence, en un point, de paires d’électrons et varie peu en présence de champs faibles. En revanche, les variations rapides de sa phase 﨏 ( る) conditionnent la circulation des courants.

Au voisinage de la transition vers l’état normal, lorsque celle-ci est du deuxième ordre, la description de G.L. permet en particulier de définir deux longueurs caractéristiques de l’état supraconducteur, la longueur de cohérence et la profondeur de pénétration.

La longueur de cohérence 﨡 (T ) définit la distance minimale sur laquelle le paramètre d’ordre peut varier; elle diverge à T ^c où les effets de fluctuations critiques sont importants. Cette longueur caractérise donc la rigidité de l’état supraconducteur.

Un champ magnétique appliqué parallèlement à la surface plane d’un supraconducteur semi-infini est exclu (effet Meissner), sauf dans une couche superficielle d’épaisseur (T ), profondeur de pénétration , où circulent des courants d’écran superfluides. Dans les systèmes de taille comparable à , le champ magnétique est donc peu exclu; cela a conduit à des mesures précises de (T ). Près de T ^c où l’«écrantage» devient faible, (T ) diverge en (T ^c 漣 T ) size=1^漣1/2 tout comme 﨡 (T ).

Quantification du flux

Imaginons un cylindre supraconducteur creux en présence d’un champ magnétique longitudinal faible H . Un circuit fermé (c) entourant le trou et suffisamment intérieur au supraconducteur ne subit l’influence ni du champ magnétique ni des courants superficiels. À cause de sa portée macroscopique, le paramètre d’ordre doit reprendre la même valeur après un tour complet le long de (c), ce qui impose une condition de quantification: le flux 淋 contenu à l’intérieur du supraconducteur est un multiple entier d’un quantum de flux 淋 ⁰,

où h est la constante de Planck et 2e la charge élémentaire des paires de Cooper.

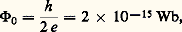Effet Josephson (1962)

Soit deux supraconducteurs, A et B, faiblement couplés, par exemple deux films supraconducteurs superposés séparés par une couche d’oxyde d’épaisseur d 年 1 nm («fonction tunnel»). Le couplage est suffisant pour que A et B puissent échanger des particules, mais pas assez pour que A et B forment un seul état quantique: les phases macroscopiques 﨏 ^A et 﨏 ^B de A et B peuvent être différentes. Il en résulte l’existence entre A et B d’un supercourant Josephson:

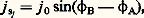qui se distingue d’un simple courant supraconducteur (lié au gradient de la phase) par ses propriétés remarquables en champs électrique et magnétique.

1. Si l’on applique entre A et B une différence de potentiel continu 嗀V , la différence ( 﨏 ^B 漣 﨏 ^A) se modifie au cours du temps t comme 2 e 嗀Vt / 寮 . Le courant entre A et B est alors:

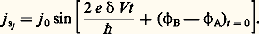On observe entre A et B un courant alternatif de pulsation 諸 = 2e 嗀Vt / 寮 . Pour une polarisation continue 嗀V égale à 1 millivolt, on a 諸 = 1,6 憐 10¹² Hz. Cet effet Josephson alternatif a été effectivement observé sur des jonctions tunnel et sur des «jonctions faibles» telles qu’un contact de taille inférieure au micromètre entre deux films supraconducteurs. Il est utilisé pour la détection d’ondes électromagnétiques, en particulier dans l’infrarouge lointain, ainsi que pour la réalisation de dispositifs électroniques. Il permet la mesure la plus précise du rapport e /h et la réalisation d’étalons de tension reliée à la fréquence par la relation 2e 嗀V = 寮 諸 .

2. En présence d’un faible champ magnétique parallèle à la jonction, le courant global maximal pouvant circuler entre A et B, à tension nulle, est:

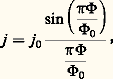où 淋 est le flux magnétique total qui traverse la jonction et 淋 ⁰ le quantum de flux. Ce résultat est analogue au résultat obtenu en optique pour la figure de diffraction donnée par une fente allongée et est directement lié à la quantification du flux: le courant entre A et B est maximal quand le flux magnétique à travers la jonction est un multiple demi-entier du quantum de flux. La pseudopériode de la variation j avec H est de quelques gauss et décroît quand on augmente les dimensions de la jonction.

Un grand nombre d’applications exploitent les propriétés de l’effet Josephson. Il est actuellement facile de réaliser des jonctions Josephson avec différents matériaux (alliages de niobium ou de plomb) de géométries variées. Un détecteur de champ magnétique extrêmement sensible peut être obtenu en reliant deux jonctions Josephson dans une boucle supraconductrice formant ainsi un Squid (superconducting quantum interference device ). Les magnétomètres Josephson permettent la détection de champs très faibles (10 size=1^漣13 T) et, indirectement, de très faibles tensions (10 size=1^漣14 V). De tels dispositifs fonctionnent également avec les supraconducteurs à haute T ^c à la température de l’azote liquide (77 K).

Un domaine prometteur pour la technologie des circuits supraconducteurs Josephson demeure celui des processeurs de signaux et de l’ordinateur avec la combinaison des temps très courts de commutation (quelque 10 size=1^漣12 s) et une faible dissipation (inférieure au microwatt). Un microprocesseur 4-bits fonctionne actuellement au Japon à une fréquence de 770 MHz.

4. Matériaux supraconducteurs

Aspect théorique

Le paramètre de Ginzburg-Landau = (T )/ 﨡 (T ), indépendant de la température T , caractérise le comportement magnétique du supraconducteur comme on le comprend sur l’expérience schématique de la figure 3 a, montrant une interface N/S en présence d’un champ magnétique. Un champ magnétique extérieur H est écranté sur une distance (T ) autour du point B, tandis que la supraconductivité, c’est-à-dire une valeur non nulle du paramètre d’ordre, est rétablie sur la distance 﨡 (T ).

La création dans un matériau initialement supraconducteur d’une interface N/S sous l’effet d’un champ magnétique appliqué conduit à un bilan énergétique que l’on peut évaluer.

Supraconducteurs de première espèce

Lorsqu’on a 麗 﨡 , plus précisément lorsque 麗 1/‘ 連2, sur la distance AB, on a perdu l’énergie de condensation en paires de l’état supraconducteur sans récupérer en échange l’énergie magnétique de volume associée à l’existence d’un champ. La création d’une interface augmente l’énergie du système et conduit donc à un état moins stable. La transition à l’état normal d’un cylindre allongé dans un champ parallèle à l’axe se fait brutalement à H ^c (courbe a dans la figure 2). Dans des géométries où il y a des effets de champ démagnétisant ^{[cf. MAGNÉTISME]}, par exemple une plaque supraconductrice en champ perpendiculaire, une subdivision de l’échantillon en régions normales et supraconductrices peut être imposée (état intermédiaire), et la transition à l’état normal se fait progressivement jusqu’à H ^c selon une structure lamellaire.

Supraconducteurs de deuxième espèce

Quand 麗 1/‘ 連2, la création d’une interface N/S permet la pénétration du champ sans trop perdre de l’énergie de condensation supraconductrice. Pour H supérieur à H ^c1, la structure est un réseau régulier de «lignes de tourbillons» ou «vortex». L’échantillon est dans l’état mixte, ou phase de Shubnikov. Une ligne de tourbillon (fig. 3 b) en milieu homogène a la symétrie de révolution d’axe parallèle au champ. Elle est constituée d’un «cœur» normal, de rayon 﨡 , où le paramètre d’ordre s’annule et où le champ est maximal. Des courants supraconducteurs circulent autour du cœur, écrantant le champ sur la distance . Chaque ligne porte le quantum de flux magnétique 淋 ⁰. En champ faible, les interactions électromagnétiques dues aux courants d’écran définissent le pas du réseau: la distance entre les lignes est de l’ordre de et H ^c1 年 淋 ⁰/ ². Le champ critique supérieur H ^c2 est atteint lorsque les cœurs de vortex se touchent, et on a H ^c2 年 淋 ⁰/ 﨡 ². Ce réseau de vortex, périodique, triangulaire, ordonné sur de grandes distances, a été visualisé grâce à une technique de décoration par des grains magnétiques (cf. photo).

Cette structure explique le comportement dynamique des matériaux de deuxième espèce dans l’état mixte. Le transport d’un courant exerce une force du type de celle de Laplace sur les lignes de flux, qui peuvent subir un déplacement avec frottement «visqueux». Cet effet dissipatif se traduit par une résistance finie et non plus nulle au passage du courant. Dans un matériau idéal, cet effet se manifeste même pour des courants faibles. En pratique, le mouvement visqueux est contrarié par un blocage des vortex sur des «centres d’ancrage» (inhomogénéités, défauts structuraux ou de surface).

Pour qu’un matériau supraconducteur soit utilisable dans des applications nécessitant des courants élevés, il faut qu’il ait un champ H ^c2 important, mais aussi des centres d’ancrage sur lesquels les vortex soient fortement piégés, d’où tout un «art métallurgique» d’introduction contrôlée de défauts.

Les métaux purs supraconducteurs sont de première espèce (sauf le niobium). Des matériaux non supraconducteurs peuvent le devenir à l’état amorphe (béryllium) ou sous pression (bismuth à 25 kiloatmosphères). On compte de très nombreux supraconducteurs de deuxième espèce dans les alliages suffisamment concentrés et les composés. La diminution du libre parcours moyen électronique raccourcit la portée de la cohérence spatiale (elle diminue 﨡 ) et affaiblit les effets d’écrantage magnétique (elle augmente ), donc fait croître proportionnellement à la concentration d’impuretés.

Supraconductivité et magnétisme

L’introduction d’impuretés non magnétiques ne change pas le couplage à spins antiparallèles d’une paire de Cooper. La température critique T ^c d’un alliage est peu différente de celle du métal pur (cf. tableau). Par contre, une impureté magnétique agit avec des forces de signes opposés sur les spins antiparallèles (Abrikosov et Gorkov, 1960). L’indium contenant 1 p. 100 de fer n’est plus supraconducteur. Cet effet est équivalent à l’effet dû à la pénétration du champ magnétique qui agit avec des forces opposées sur les électrons de moments d’impulsion opposés. Au voisinage de la transition du deuxième ordre à l’état normal (à la concentration critique où s’annule T ^c ou au champ critique H ^c2), la bande interdite du spectre d’excitation s’annule.

Une nouvelle classe de matériaux ternaires (phase de Chevrel) de la forme TRMo⁶X⁸ (TR = terre rare, X = S ou Se) montre la coexistence simultanée dans un même volume de la supraconductivité et du ferromagnétisme, et renseigne sur la compétition d’éloignement des spins électroniques due à ces deux mécanismes. Par contre, la coexistence de supraconductivité et d’ordre antiferromagnétique observée dans plusieurs systèmes est tout à fait compatible avec un alignement à spins antiparallèles.

Supraconducteurs à haute ^c

Les matériaux supraconducteurs à haute T ^c appartiennent à la famille des cuprates, dont la structure cristallographique de type perovskite est caractérisée par la présence de plan cuivre-oxygène (plan CuO²). Le nombre de plans Cu² dans la structure de base varie d’un composé à l’autre ainsi que le couplage entre les plans Cu² qui peut être modifié par l’introduction de plans intermédiaires d’autres éléments chimiques. Le composé YBa²Cu³⁷ comporte deux plans Cu² séparés par le Ba; dans les composés plus complexes de la forme Biⁿ Sr²Caⁿ size=1^漣1Cu^{n 2n + 4}, n plans Cu² (n = 1, 2 ou 3) séparés par les plans Sr sont regroupés. Le caractère bidimensionnel très prononcé des cuprates est responsable des propriétés anisotropes de ces matériaux et joue certainement un rôle prépondérant pour la supraconductivité. L’existence de cette structure en couches explique qu’un courant électrique passe difficilement dans une direction perpendiculaire aux plans. L’anisotropie cristalline est également responsable des valeurs différentes de la longueur de cohérence selon la direction parallèle aux plans ( 﨡 黎 1,5-2,0 nm) et perpendiculaire (0,3 nm) pour le composé YBa²Cu³⁷, ce qui modifie la morphologie des lignes de flux. Lorsqu’elles sont perpendiculaires aux plans Cu², elles sont divisées en petits éléments très mobiles entre les plans, diminuant ainsi le courant critique.

La nature lamellaire des cuprates est exploitée pour synthétiser ces matériaux sous forme de films. Ceux-ci supportent des densités de courant très élevées, de l’ordre de 50 000 A/mm² à 77 K.

Le tableau indique les grandeurs caractéristiques de quelques supraconducteurs typiques.

5. Applications

L’intérêt technologique des matériaux supraconducteurs «durs» (NbZr, NbTi, Nb³Sn) réside dans l’obtention de champs critiques élevés (20 T à 4,2 K) et de grandes valeurs de leur densité de courant critique. Ainsi Nb³Sn ne retourne à l’état normal que pour une densité de courant supérieure à 4 000 A/mm² dans un champ magnétique de 5 T. Les dispositifs à supraconducteurs se rencontrent essentiellement dans des domaines où les contraintes économiques ne sont pas importantes (recherche-développement, etc.), car le besoin d’une réfrigération pénalise les petites applications industrielles.

Bobinages supraconducteurs

Les aimants supraconducteurs sont utilisés dans des domaines nécessitant de forts champs magnétiques dans des volumes parfois importants (stockage d’énergie, fusion thermonucléaire contrôlée, chambre à bulle). L’aimant qui entoure la chambre à bulle du Cern, à Genève, a un volume utile de 80 m³ et un champ maximal de 3,5 T. Les câbles supraconducteurs utilisés ont une structure multifilamentaire; l’introduction contrôlée de défauts et les structures composites permettent un piégeage important, nécessaire pour avoir de forts courants critiques, et limitent les «sauts de flux» qui causent un échauffement local jusqu’au voisinage de la température critique.

Machines supraconductrices

Les alternateurs à inducteur tournant supraconducteur et les moteurs continus (fondés sur le principe du disque de Faraday) deviennent avantageux dès qu’on s’intéresse à des puissances élevées (10⁹ W) ou à de faibles poids. Signalons aussi la réalisation de cavités supraconductrices hyperfréquence à coefficient de surtension élevé et la réalisation d’accélérateurs linéaires de particules supraconducteurs.

Câbles de transmission de courant

Pour avoir des courants élevés sans dissipation, on recherche des matériaux où les lignes de vortex soient fortement piégées ou encore du niobium au-dessous de H ^c1. Compte tenu de la réfrigération, le prix de revient d’une ligne de 1 000 km ayant une capacité de 10¹¹ W serait inférieur d’environ 50 p. 100 au prix des lignes conventionnelles.

Développements futurs

De nombreuses applications industrielles faisant appel à la supraconductivité sont actuellement à l’étude dans les secteurs du transport (train à lévitation magnétique, bateau à propulsion magnétohydrodynamique), de l’énergie (stockage de l’électricité), de la médecine (capteurs magnétiques ultrasensibles pour l’imagerie médicale), de l’électronique (convertisseurs analogique-digital ultrarapides), etc. L’avènement des supraconducteurs à haute T ^c a modifié profondément les limites de rentabilité de tels systèmes grâce à l’utilisation d’un fluide cryogénique peu onéreux (l’azote liquide). Si les difficultés de mise en forme de ces matériaux sont résolues rapidement, une véritable révolution technologique fondée sur la supraconductivité verra le jour au XXI^e siècle.

supraconductivité [ syprakɔ̃dyktivite ] n. f.

• 1927; de supra- et conductivité

♦ Phys. Phénomène par lequel la résistivité de certains matériaux (supraconducteurs), après avoir décru régulièrement à mesure que leur température s'abaissait, tombe brusquement à une valeur proche de zéro.

● supraconduction ou supraconductivité nom féminin Phénomène présenté par certains métaux, alliages ou céramiques dont la résistivité électrique devient pratiquement nulle au-dessous d'une certaine température (appelée température critique).

supraconductivité supraconductibilité ou supraconduction

n. f. PHYS Conductivité très élevée que présentent certains corps aux températures voisines du zéro absolu (zéro kelvin).

supraconductivité [sypʀakɔ̃dyktivite] n. f.

ÉTYM. 1927; de supra-, et conductivité.

❖

♦ Phys. Propriété d'un corps qui présente le phénomène de supraconduction. || « (…) des recherches considérables sont menées en vue d'affranchir un jour la supraconductivité d'une utilisation onéreuse des fluides cryogéniques comme l'hélium ou l'hydrogène liquides (…) pour l'instant, la température critique de tous les supraconducteurs connus reste limitée à 23,2 K » (la Recherche, n^o 50, juil.-août 1974).

Encyclopédie Universelle. 2012.